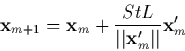Review of the RGF procedure by Quapp and Hirsch
In the RGF method the gradient criterion for stationary points
the gradient criterion for stationary points
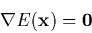 |
(1) |
is reduced by one equation leading to
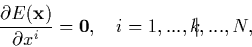 |
(2) |
where the vector x represents the nuclear coordinates.
The omitted coordinate k defines the search direction.
This was generalized by the projector equation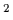
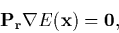 |
(3) |
where
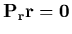 with a fixed search direction
r.
Note that Eq.(2) is a special case of Eq.(3) with the corresponding
with a fixed search direction
r.
Note that Eq.(2) is a special case of Eq.(3) with the corresponding
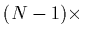
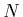 projector matrix
projector matrix
thus, 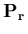 is built by the unit vectors orthogonally to the search
direction, where here again the k th unit
vector is missing.
Another possibility to define
is built by the unit vectors orthogonally to the search
direction, where here again the k th unit
vector is missing.
Another possibility to define 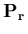 is to use the dyadic product in
is to use the dyadic product in
where 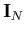 is the unit matrix.
It is an
is the unit matrix.
It is an 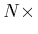
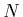 matrix of rank
matrix of rank 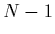 .
.
The reduced gradients of Eq.(3) define curves connecting stationary
points.
Starting from a given point (e.g. a minimum) one follows a selected
curve to reach the saddle point of interest.
A predictor-corrector method is used for tracing these curves.
Assuming a curve of points x(t) fulfilling the N - 1 conditions of
Eq. (3),
the tangent x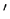 to the curve is given as
to the curve is given as
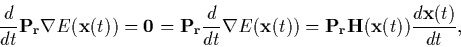 |
(4) |
or
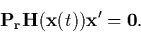 |
(5) |
This is a homogeneous system of N - 1 linear equations where the coefficients
are the elements of the Hessian matrix H projected by
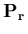 . Eq. (5) is solved using a QR decomposition.
. Eq. (5) is solved using a QR decomposition.
In the predictor step the sequence of points x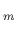 and x
and x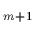 is computed as
is computed as
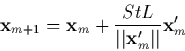 |
(6) |
where StL is a steplength parameter.
Since the new point does not satisfy exactly the condition defined
in Eq. (3), a corrector step is added in which Eq. (3)
is solved using a Newton-Raphson-like method.
In general, the linear
combination r of internal coordinates is used as initial
search direction.
The use of the metric in internal coordinates is explained in the appendix
of Ref. A quite better combination of predictor and corrector steps is applied in
Ref.4.
A quite better combination of predictor and corrector steps is applied in
Ref.4.
1 Quapp W, Hirsch M, Imig O, and Heidrich D,
J. Computat. Chem. 19, 1087 (1998)
2 Quapp W, Hirsch M, and Heidrich D,
Theoret. Chem. Acc. 100, 285 (1998).
3 Hirsch M, Quapp W, and Heidrich D, Phys. Chem. Chem. Phys.
1, 5291 (1999).
4 Hirsch M, Quapp W, J. Computat. Chem. 23, 887-894 (2002)
Home
w.q.
2001-09-03
![]() the gradient criterion for stationary points
the gradient criterion for stationary points